プロジェクトメンバー

• Kai ZHANG　Kai ZHANG
  システム情報工学研究群 社会工学学位プログラム
• 高野 祐一　Yuichi TAKANO
  システム情報系／人工知能科学センター（サービス工学分野）
• Yuzhu WANG　Yuzhu WANG
  システム情報工学研究群 社会工学学位プログラム
• 吉瀬 章子　Akiko YOSHISE
  システム情報系／人工知能科学センター（サービス工学分野）

研究概要

Background

Mobility as a Service (MaaS)

• build a seamless and integrated multimodal mobility system.
• promote some emerging mobility services, such as carsharing.

Emerging Carsharing Services (Figure 1)

• provide a potential solution to first- or last-mile problems.

Society 5.0 in Japan

• make movement smooth by combining carsharing services, public transportation.

Our Research

Focus on one-way station-based carsharing systems.

• One-way trips usually occupy a large proportion of trips.
• Operators can manage vehicles more easily.

Present a two-stage risk-averse model.

• Risk measure: Conditional Value-at-Risk (CVaR) (Figure 2)
• Strategic decisions: station locations, station size and fleet size

Develop two algorithms to solve the problem.

• Branch-and-cut: handle the nonlinear CVaR function.
• Scenario decomposition: handle the special block-angular structure of the problem.

Conduct the experiments based on the data from Ha:mo RIDE, Toyota.

Experimental Results

• Efficient frontiers of mean return and conditional value-at-risk (CVaR) for different confidence levels β (Figure 3)
• Optimal station locations and capacities for different weights λ between return and risk (Figure 4)

Figure 1: Toyota Ha:mo RIDE carsharing, Japan

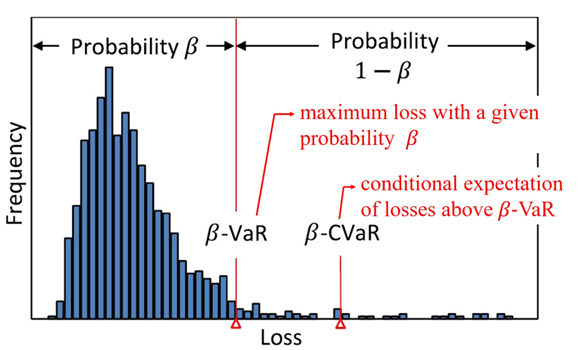
Figure 2: Value-at-Risk (VaR) and Conditional Value-at-Risk (CVaR)

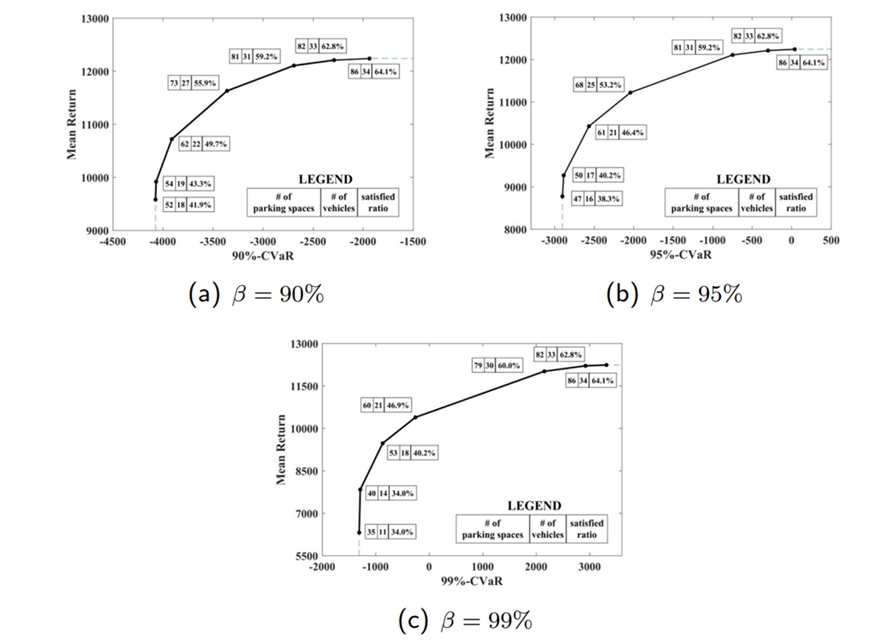
Figure 3: Efficient frontiers of mean return and conditional value-at-risk (CVaR) for different confidence levels β

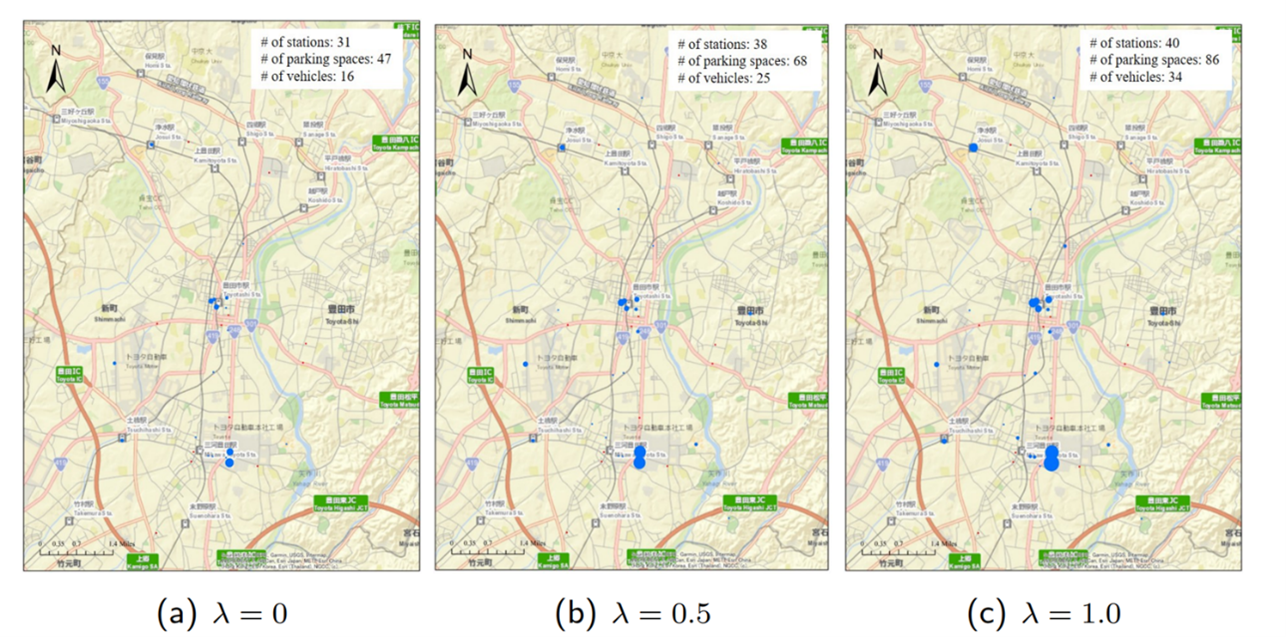
Figure 4: Optimal station locations and capacities for different weights λ between return and risk

参考文献

[1] Zhang, K., Takano, Y., Wang, Y., & Yoshise, A. (2021). Optimizing the strategic decisions for one-way station-based carsharing systems: A mean-CVaR approach. IEEE Access, 9, 79816-79828.